≪1≫ 平面でのn角形はあんまり(というか、ほとんど)面白くありませんが、一個次元の上がった立体のn面体となりますと俄然面白くなってきます。さしあたっては、n面体にはどんな種類があるのか?を考えていきましょう。
≪2≫ よく知られているように、4面体は「三角錐」の1種類、5面体は「三角柱」「四角錐」の2種類であります。

記号ですが、5A(2,3)とかは5面体の一つ目の種類であって、その面の構成は三角形が2面と四角形が3面でできてますよーという、自家製の記号です。
では6面体は何種類あるでしょうか?という問題が、むかしの大数(大学への数学)の宿題に出題されました。→参考図書[1](なんと50年近くまえ・・・)
≪3≫ 標準的な解法としては、オイラーの多面体定理等で条件を絞り可能性のあるものについて実在性を確認するというのがありますが、対極的手法として「すべてのn面体は、n-1面体を平面で切ることで得られるのだ」という箇条を信じ、ひたすたぶった斬るという直感主義的手法があります。
以下では、5面体の5Aおよび5Bの各頂点のところを斬りまくってみました。(当時のメモを整理したもの) 頂点を含む平面で斬るのですが、既存の平面が無くならないところまで斬っていきます。立体図の右脇のダイダイ色の図によって組合せぐあいなどを確認します。6A、6Bなどが新種の意、=記号は、既出という意味合い、×印は平面が成立しないのでダメという意味です。


というような感じで、結局6面体は6Aから6Gまでの7種類が出てきました。(立体図で1面を塗りつぶしてあるものがそれ) 一点、6Cでaとbは鏡像と見受けられますが、上記[1]や一覧表のあるガイ他[2]、宮崎[3]においても「7種類」ということで、鏡像は同一視が主流のようです。(鏡像ですよね?)
≪4≫ さらに進んで7面体は何種類?と斬りまくり、30種ていどをピックアップしていたところ、書店で前掲[2]の一覧表(12面体までの表)に出くわし、斬りまくるのは中断した次第です。
≪5≫ 7面体におきましては、[1]や[2]、宮崎[3]にも注意がありますが、下図のように「同位体」のようなものが現れるようです。7点7面体(オイラーによる呼称)とも呼ばれ、三角形、四角形、・・・の個数は、いづれも(4、3、0、0)です。辺の数もオイラーの定理から7+7-2=12ですが、各点に集まる辺の数が異なるようです。
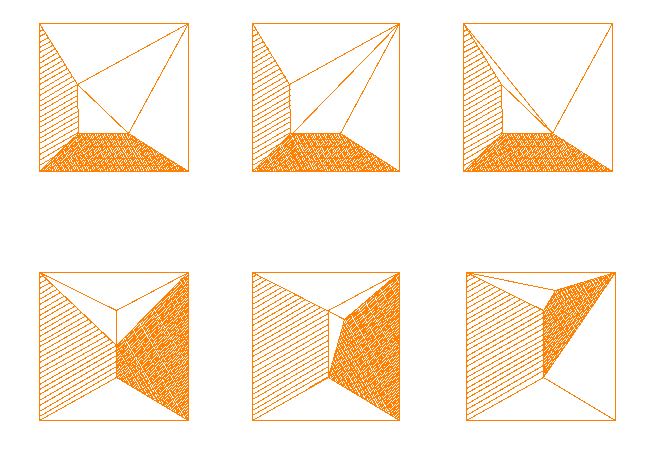
上図では、どれも3枚あるという四角形のうち2面を塗りつぶしておきました。(もう1枚は外枠の正方形) これで組合せ方がちがうのが分かりますが、すべてかどうかは不明です。
さらに8面体になると、下図のようなものも登場するとのこと。これらの「区別」も(建築等への応用面からしても)必要になろう、との宮崎先生のお言葉でありました。

≪参考図書≫
[1]大学への数学、宿題、東京出版、12-75出題、02-76解答
[2]R.K.ガイ他著、秋山仁訳、幾何学における未解決問題集、1996、シュプリンガー(p103に「与えられた個数の頂点と面を持つ組合せ的に異なる多面体の個数」の表があります。10面体は3万種以上、12面体は600万種以上とのことであります)
[3]宮崎興二、多面体と建築、彰国社、1979(とくにp283~) かたちに関する本をいっぱい出されている宮崎先生の一冊です。