≪1≫ 平面図形でその面積と全周長が、数値的に一致するような図形を、戸村先生は 「超図形」(ultra図形)と命名されました。[1]ここでは、n次元の場合の「超球」とかの呼称と紛らわしいので「ultra」を使用したいと思います。
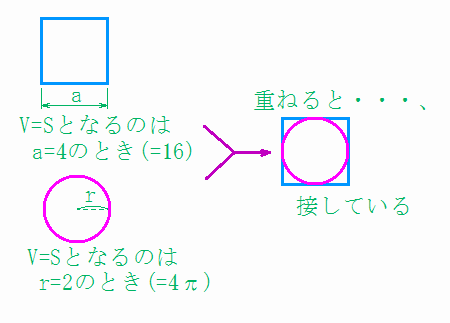
たとえば、一辺の長さが4である正方形では、面積は4^2=16、全周も4×4=16となり、これが「ultra正方形」となるわけです。
同様に「ultra円」を探してみると、半径をrとして、πr^2=2πrから、r=2が該当することが分かります。
いま求めた「ultra正方形」と「ultra円」を重ねてみますと、両者は「接している」ということが観察できるわけです。
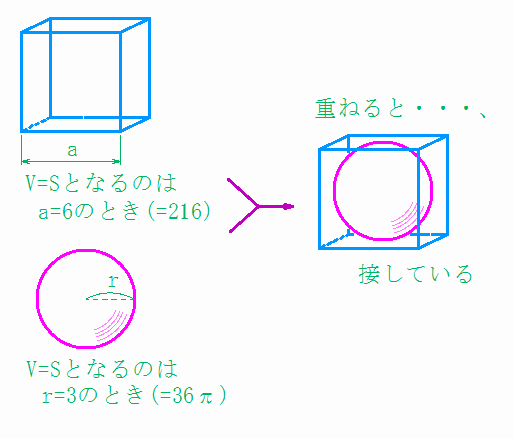
≪2≫ では、立体ではどうか?と思うのは自然な発想。で、立方体では、面が6個あることなどから、aの方程式
![]()
の解としてa=6が該当。他方、球では中学生必須の暗記式の登場でrの式
![]()
の解でr=3が出てくる。ここでも、やはり両者は接していることが分かります。
≪3≫ 一般のn次元における立方体と球ではどうなっているのか?と思うのは至極自然な発想。立方体のほうは式
![]()
より、一辺a=2nのときに;いっぽう球のほうは(いささか牛刀っぽいですがby Wolfさんから)式
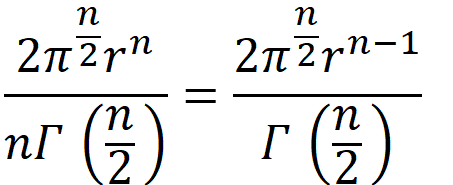
の解で、半径r=nのときに両者がultraになり、このときa=2r;すなわち 「一辺=直径」となり、両者はやはり「接している」ことになります。
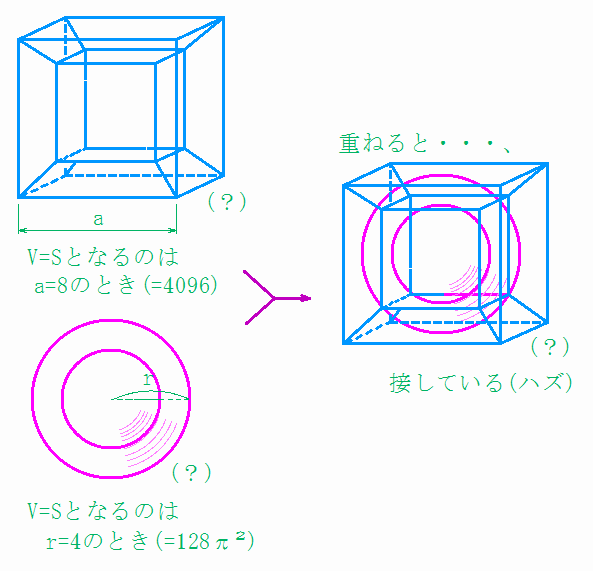
(・・・4次元の球って、こんなんでしたかね?)
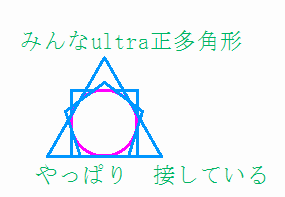
≪4≫ いきなりn次元に行っちゃいましたが、ちょっともどって、平面の正多角形の世界ではどうでしょうか?
ここでも一辺の長さがaのultra正n角形は、面積=周長の式;
![]()
から一辺a=4tan(π/n) となります。(cotはtanの逆数)このときの「辺芯距離」(by Wolfさん用語、ふつうには内接円の半径)は一般に
![]()
とのことですので、これに先ほどのa=4tan(π/n) を代入しますと、nにかかわらずいつも2、すなわちultra円の半径と等しくなり、いつも(正なに角形であっても)「接している」ことが観察されます。
≪5≫ ここまできますと、(5個しかないといわれる)正多面体ではどーなっているのかと気になるのが、いけないクセです。ここでは恒例のWikiさんに活躍いただき、体積や面積の式を活用させていただきたいと思います。
ここでも同様の計算でもって、r=3のultra球には、どんなultra正多面体も接していることが分かります。計算の方針は以下の通り。
1.体積=表面積の方程式から、ultraの場合の一辺の長さaを求める。
2.内接球の半径の式に、上記のaを代入する。
3.半径を計算すると、5つともr=3となる。
(正12面体のときは計算がややメンドウですが…)
たとえば、ultra正20面体は、一辺a=3.96950…のときで、
これはr=3の球に接している、、、。(このa=3.96…は代数的数です、念のため)

つまり総じて、ultra図形は、よい図形である、といえると思うんです。
本日もご静読、ありがとうございました。
参考書
[1]戸村浩、超平面‐円、数学セミナー3-77、TOMのページ、日本評論社
[2]ほか、数学セミナー2-77,5-77,3-79など。
もろもろの発端は[1]です。
[3]上掲のWiki、Wolfご両名。 いつもありがとうございます。
改定
2024.02.16 図がみにくかったので明確化、文章も少々見直しました。