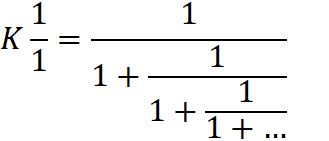笹の葉 さらさら ～七夕によせて

≪１≫　昨日が七夕だったわけですが、じぶんがむかしからちょっと気になっていたグラフで、ｙ＝tanｘの逆関数みたいなのん、つまり　　　　

　　　　値域は　－1＜ｙ＜1、でｙ(0)＝0、

　　　　導関数は全域ｙ’＞0の単調増加、原点ではｙ’(0)＝1、

(+条件アルファ)ってなるグラフは、どんなのがあるんやろう？

　　　　

ということで、恒例のGeoさま援用で６種かき集め、七夕の短冊風に色をつけて並べてみました。

　（なおこういう関数って、なんか名まえが付いていた記憶もあるんですが、スイマセン、ちょっと探しきれませんでした。→【8/19追記】へ）

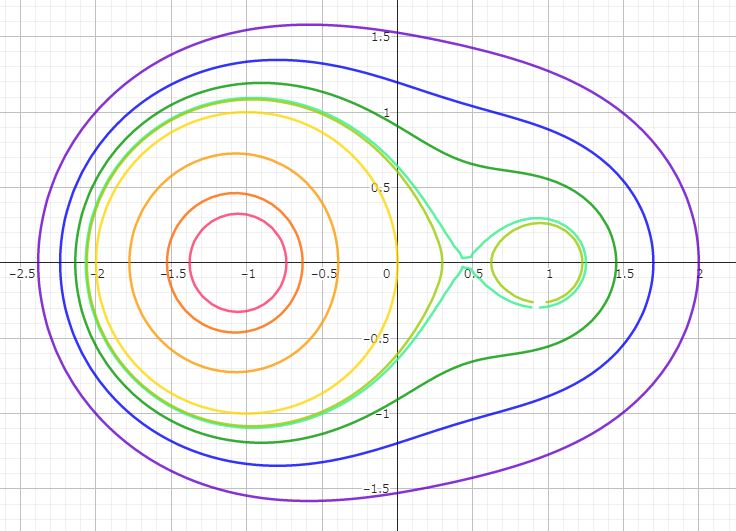
≪２≫　何はともあれさっそく、その６種さんに登場いただきましょう！

　　　　

そしてｘが0から0.5あたりまでの拡大版も：（NHK朝ドラらんまんの槙野万太郎が、植物にぐっと近寄って観察するイメージですなぁ）

　　　　

花火のように発射された曲線ですが、なかには先々で交わっているのもあるようです。

　。。。ふるさとの学校を卒業した人々が、各人社会に出て大小さまざまな人生を過ごし、ときには交わりながら生きていく。そうしてやがては、すべての人は(ｙ＝１へと)天寿をまっとうしていく。だれしも。。。

　おっとぅ、老爺の感傷に浸るまえに、青少年のみなさんにはそれぞれの数式を明示しておくべきでしたー。

　　　　

　　　　

　　　　

　　　　

　　　　

　　　　

ぜんぶ、ｘが正の範囲での式ですね、ねんのため。（負のほうは、少々小細工必要）

ｙ１とｙ２、ｙ３とｙ６は親戚みたいな感じですね。検証や式変形は各自、試みてみてくださいませ。（あってるかな？）

また、根本的にちがう他の例を見つけられたら、ご教示いただきたいのです。

【7/9　追記】

　ほかの１例ですが、たとえばガンマ関数のｘの区間が［0，1］の部分を頂戴しますと

傾き Γ’(1)＝－γ（オイラーの定数）に留意して、

　　　　

すなわち、

　　　　

といった表記のものもございますネ。（逆関数ー1表記の下は、区間のつもりです。いつものように自家製の表記デス）

　このように、漸近線のあるものをターゲットにするともっといろいろありそうでウレシイです。

【8/19追記】

　最初に「なまえがわからない」としていましたが、ひょんな拍子で判明、「シグモイド曲線」とか。

ja.wikipedia.org

おまけに、６種のサンプルカラーグラフ「ς型の関数の比較」もあり、サンプルの個数といい、カラーリング感覚といい、まったく同様なものでした。

　正式に数学的性質を追及されたい皆様は、本家Wikiさんのほうから探求されますようご案内しておきます。（追記おわり）

以上、御静読ありがとうございました。

≪追伸≫　本日7/8の読売新聞夕刊に、めづらしく数学記事が！しかも社会面。

例の京大望月先生のABC予想の「証明」に、欠陥を見つけたら１億４千万円の賞金を、他方、理論の発展論文には1400万円を、それぞれある団体さんが寄付しますと。

たしか、フィールズ賞が約200万円なので、上記のようなテーマに人生を賭けるほうがカネ目当てなら得策かもしれません。っていうか、お金持ってる人は本家フィールズ賞のほうに寄付して、もっと賞金を上げてほしいものですね。

あっ、ちょっと生々しい感じになってきちゃいましたので、このへんで😅

続・ある２数の大小問題

≪１≫　本日は「ある２数の大小問題のこと」(５/２８)の続編、、といいますか、その周辺情報を書き留めておきたいと思います。

≪２≫　まずは、Wolfさんに「ｘ^ｙ＝ｙ^ｘ」と入力すると、いきなり登場します下記の陽なる表示式；

　　　　

これを数値上で再確認してみました。W(　)は、”ランベルトのW函数”  とかいう高尚な関数とのことですが、説明は愚生には手に負えませんので、

ja.wikipedia.org

あたりを参照願います。

　この式が、前回のような（Geoさんの）グラフになるのかどうか？ですが、エクセル風の表計算LibreCalcでカタカタっとやると、おおむね

　　　　

　　　　

めでたく「双曲線」風のかんじになり、数値も（２，４）の組や、（ｅ、ｅ）なども通過していますので最初の式でやっぱし相違なしのようです。

　前回記事の最後の数値の例；

　　　　√３^５　と　５^√３　ではどちらがおおきい？

ですが、y=5となるようなｘはというと、上表から

　　　　ｘ＝1.76495…

となり、√３＝1.73201…よりは大きくなっています。（下のミドリの点、あかの点。）

　　　　

つまり、これは水面下＝マイナスの領域にある組み合わせとなりまして、結局、指数の大きいほうが逆に小さい；

　　　　√３^５＝15.58845･･･

　　　　５^√３＝16.24245･･･

　　　　すなわち、　√３^５　＜　５^√３

となることが分かります。（もっとも、数値大小だけならこんなことやるより電卓でやるほうがはやいですが…😅）

≪３≫　さらなる余興ですが、かかる曲線が「双曲線」に似ているとのことで、その双曲線を赤点線にして比べてみました。（式はグラフ中に表示しています。）

　かなりニアーではありますが、でもやっぱりちょっと違うというのが目視観察でもわかり、じわりました。たとえばｘ＝４のとき、本家の式ではｙ＝２ですが、こちらのモドキ式ではｙ＝1.98416…と。。。

　こんごは、このわずかに見えるスキマの面積が、はたして収束するのか否か？あたりも探求していきたいと思っております。

　　　　

　以上のご静読、ありがとうございました。

参考資料

［１］W関数の数値は、CASIOのkeisanサイトを使用させていただきました。

作者: tonagai さん。

keisan.casio.jp

今回は、ここでの計算結果を上記の表計算にせっせとコピベしてこしらえました。表計算で実装されてれば最高なんですが。。。（されてる？）

なおこのkeisanは、W関数以外にもみんなの自作式とかもあり、愚生のお気に入りのページのひとつとなっております。

［２］森口他、数学公式Ⅰ、岩波全書（2020）

これのｐ281にも「x^y＝y^x」のグラフが載っていました。さすが公式の鬼。

むかしの先生方も、やはりこんなんにも興味をもっておられたことが感じられ、うれしいです。

ある２数の大小問題のこと

≪１≫　「なんとかの何乗」というベキ演算では、交換法則が成り立たないのをいいことに、 ａ^ｂ と逆にしたｂ^ａとの大小問題がよくお目にかかりますね。有名どころでは、

　　　　

　　　　

　　　　

といったものです。［１］～

　これの定番解法というのは、対数をとって比較するんだということで、関数ｙ＝ln(ｘ)/ｘがｘ≧ｅでは

　　　　

と単調減少ですんで　ａ、ｂを ｅ≦ａ＜ｂ とした場合には、 ln(ａ)/ａ＞ln(ｂ)/ｂ　つまり　ａ^ｂ＞ｂ^ａ　となるということで、はやい話が「指数が大きいほうが大きい」ということです。（両方ともｅより大きい場合です）冒頭の３例はそういう例ですね。

　同様にしてａ、ｂがともにｅより小さいときは大小が逆転し、こんどは底数が大きい方が大きいとなるわけです。

　　　　

【6.11 修正です】

　　　　　　　　（ɤはオイラーの定数）　　　　等々。

　　　　πはｅ以上でした😅　例としては、かわりに ２ としておきます。

　　　　        　　（引き続き、ɤはオイラーの定数）

≪２≫　状況を俯瞰するためにつぎの、２数の差の関数をもってきましょう。

　　　　

いきなりですが、これを３DーGeoさんに描画してもらいます。（見やすくするためですが高さｚ軸方向は少々縮めてあります。）

　　　　

ちょっとｘ軸に沿った山脈みたいなところの向うがわかりにくいので、視点を変えるとこんな感じです。座標でいうと（15，10，10）あたりから見る。

　　　　

　ここで観察されることは、

　　　　・ｘ^ｙ＝ｙ^ｘとなる、すなわち ｚ＝０ となるのは、グラフで「海岸線」風

　　　　　に見える個所のハズだ。

　　　　・それはｙ＝ｘはアタリマエとして、なにやら双曲線っぽい曲線上でも等しく

　　　　　なっている。２^４＝４^２などは、この曲線上にあるハズ。

　　　　・交点は（ｅ、ｅ）っぽい。ｘ＝１，ｙ＝１が漸近線。

　　　　・（ｘ、ｙ）での値と（ｙ、ｘ）での値は＋－が逆。つまり奇関数ふう。

　ここで２数が等しくなるという「海岸線」をピックしてみます。つまり、ｘ＝ｙなら当然２数は等しいのですが、あとｘ≠ｙでも ２^４＝４^２みたいに等しくなる点が、反比例みたいな曲線（きみどりの曲線）上に乗っかっていて、その付近では大小の区別が発生しているという状況です。

　いま奇関数性のため、ｙ＞ｘつまりｙ＝ｘより上側のみを対象としましょう。そしてｘもｙもｅ（むらさきの線）で区切ると４つの領域に分かれます。領域①②は「指数の大きい方がおおきい」、領域③④は逆のエリアです。

　サンプルの点でいいますと、A点は　π^e＜e^π、Ｂ点、Ｃ点も上記の点となります。

　　　　

≪３≫　はじめの関数ｙ＝ln(ｘ)/ｘで判別できるのは、領域①と領域④となりますね。

逆にこれでは判定不能な、③や②、あるいは曲線付近のキワドイ２数をもってきて大小を比べてみるという新種の楽しみ方もできます。

　たとえば、√３と５とかで、数値的には、

　　　　√３^５＝15.58845･･･

　　　　５^√３＝16.24245･･･

となりまして、指数の大きいほうが小さい、つまり負の領域③に属しているという感じです。

　こんごは、このあたりの判別方法を模索するということで苦悩して（楽しんで？）いきたいと思っております。

　御静読、有難うございました。

≪参考書≫

［１］鈴木貫太郎「大学入試数学　不朽の名問100」(ブルーバックス、2021)、ｐ167～

［２］一松信、牛島照夫「数学の問題第３集」(数セミリーディング、1988)､問27，76

　などなど。

似ている数の例示

≪１≫　連休初日、どっかへ行きたいところですが、そこはガンマ、、、いやいやガマン。

で、以前にnet内か、どこがで拝見したパズル風数値式を、紹介しましょう。

まずはｆ（ｘ）を次式とします。

　　　　

このとき、ｘに1/2、1/3、－(ｅ)√ｅ（マイナスｅのｅ乗根）を代入すると、

　　　　

　　　　

　　　　

ムムム、見覚えのある数値、定数界の東西正横綱＆東の張出横綱のお出ましのようです。（ただしモドキです）

念のため、正真正銘の３横綱値とさせるｘは？というと、順に

　　　　0.49837･･･（ ≒ 1/2  ）

　　　　0.33986･･･（ ≒ 1/3  ）

　　    －1.43360･･･（ ≒ －(ｅ)√ｅ  ）

ですとのこと。（by  Wolfさん）

≪２≫　近似の ” ほとんど整数 ”  という世界では、０や９が何個並んでいるか？なんて表現がなされます。数 α とその近似値ａの差の絶対値で、単純に０や９が並んでいる個数を、ここではｇ（ α 、ａ）としてみます。（ｇに深い意味はありません）

たとえば、

　　　　ｇ（ π 、22/7）＝２　(有名な近似値)

　　　　ｇ（ π 、355/113）＝６　（同上）

というかんじです。いってみれば、（差での）「近似度」。

　上記はじめの３例は、ｇ＝２、１、２となりまして、近似値というにはややさみしい感じですね。

　π や e ではありませんが、古いノートとかにはこんな近似例がありました。

　　　　ｇ（ ɤ 、ln(34/9)/ln10）＝４　

　　　　ｇ（∑(1、∞)1/(ｎ！)^ｎ、√√(223/90)）＝６

　　　　ｇ（Ｔ(1、∞) 1+1/ｎ、466/133）＝４　

　　　　　　　（Ｔはタワーベキをあらわす自家製記号）

　　　　ｇ（ π^76/ｅ^87 、１）＝３

　　　　　　　（1年ほど前の小ブログ）

　なお、（　）内の数式をこう書くとイマイチありがたみが薄れますので、ふつーの書き方で書いておきますと、

　　　　

　　　　

　　　　

　　　　

となりますね。

≪３≫　何かに近いというのは、差や商を取ると０や１に近くなるということで、WikiさんやWolfさんにも「ほとんど整数」という興味深い名称の項目があるのは、みなさま　ご承知かと。

　有名なところを再度、何品かをｇで表してみますと、

　　　　ｇ（ｅ^(π√163)、[左記](＝左記の整数部)）＝12

　　　　ｇ（ｅ^π－π、20）＝3

　　　　ｇ（sin11、－1）＝5

等となります。

≪４≫　少々脱線ではありますが、近似度をあらわすｇの概念を少々延長して、なんらかの命題にたいして、その初例からの連続適合事例の数をあらわすもの、としてみます。開幕からの連続試合安打みたいな。

　有名どころから例をもってきますと、

　　　　ｇ（ｎ≧２にたいし、ｘ^n+ｙ^n＝ｚ^nは自然数解をもつ）＝1

　　　　　　　（ｎ＝２のみ適合。フェルマーの定理 ）

　　　　ｇ（ｎが素数なら2^n-1は素数になる）＝4

　　　　　　　（メルセンヌ素数。p5＝11でストップ）

　　　　ｇ（ｎ≧２にたいし、ζ(ｎ)は無理数）≧3

　　　　　　　（現在、ζ(５)が不明。ここは、おそらく ＝∞  でしょうが･･･）

　命題のときに初めの何個かの適合例だけではなんとも言えないよねというのは、世間でも十分警戒されていると思われます。たいして、数値の場合は、≠  は前提として「なぜ、似ているのか？たまたまか、または理論づけできるのか？」という点が大切にされている感じがしています。参考資料［４］に、数値ハンターへの教訓のことばが載っています：

　　　　「何かに似ている答えを得たら、それは違う」

　もっとも数値の場合はパズル的側面もあり、愚生はリラックスできる対象として捉えており、これでもって大型連休も楽しめるのではと計画しておる次第です。

〈参考資料〉

［１］どこかで出会った「√２+√３≒  π」の記事（出会われた方がいらっしゃたら

　　　一報をお願いします）

［２］記事：ほとんど整数、Wiki；Wolfram など

［３］my  note、ふるいノート

［４］ジョナサン・ボールウェイン、キース・ブリデン、数学を生み出す魔法のるつぼ、オライリー・ジャパン、2009，ｐ94（この本、アマゾンでの読者評は翻訳がマズイと酷評されてますが、内容のほうはとてもおもしろいと感じております。）

距離のベキが一定な曲線を回顧する

≪１≫　平面上に２点があって、そこからの距離の 和  が一定な曲線は？といえば、楕円。 積  が一定なら？といわれりゃレムニスケート！

なら、ベキならどうなの？という記事が、これまた半世紀まえ（正確には45年前）の雑誌「現代数学」［１］にありました。

　記事の著者山下先生も、当時の最新型計算機？HITAC-10を最大限に活用されて数値の計算やそのグラフ化をされておられ、いま読み返してみますと計算機性能の違いにやはり隔世感を味わえ、じわります。　

　　　　

（写真はweb「日立評論1969年11月号:超小形電子計算機 HITAC 10」より。当時価格で、約500マンエンとのことデス。）

　本日は、ベキの場合を今日的アイチムでもって焼き直してみて、数値や形状グラフを再堪能してみるという回顧型記事となります。

≪２≫　２点を（-1，0）,（1，0）とれば、距離はそれぞれ

　　　　Ａ＝√((ｘ+1)^2+y^2)、Ｂ＝√((ｘ-1)^2+y^2)

となり、式Ａ^Ｂ＝ｃを満たす点の集まりが、今回の曲線となる。

　当時の記事では、まずはｃの値ごとに該当点（ｘ、ｙ）を平面上にプロットしていくというなかなか手の込んだ手法で概形を推測していくという方法ですが、当時はこれしかないので致し方ございません。

　ここは是非、若い読者のみなさんにも、当時の昭和の苦労感を堪能してもらえればとの意向で、記事の図の一部を引用させていただきましょう。

　　

こういうのをいっぱい作成して、やっとこさ次のような予想概形の図にたどり着く、というプロセスになる。

　　　　

ｃの値は、外側から順に

　　　　3、2、1.5、

　　　　1.22676･･･、

　　　　1、0.5、0.2、0.1、0

で、1.22676･･･のところでレムニ型が生成されているのが観察されます。

　概形がつかめたら次はレムニスケート風になりそうなポイントを正確に探すために、

稜線ｙ＝０での切断面のグラフと、あと、それを微分した式＝０から極点を導出するという王道手順。つまりｙ＝0とした    の極点を捜索していくことになります。（タテ軸がｃです）

　　　　

　ここで、Wolfさんらにも登場いただき算出された各数値を比較してみて、正確さの「経年優化」のどあいを見比べてみましょう。まず極大となるｘの値はといいますと

　　　　・記事    0.45473  321･･･

　　　　・Wolf    0.45473  32175  61064･･･

　　　　・Geo     0.45473  32176  185･･･、

また、このときのｃの値は

　　　　・記事    1.22676  213･･･

　　　　・Wolf    1.22676  21178  23279･･･

　　　　・Geo     1.22676  21178  233･･･

となっていて、小数点以下７位くらいまでは当時のものでも正確だと見受けます。なお、Geoさんで表示してくれるextremumエクストゥリマム（極値）も、いつもですが、同じく７位くらいまでが正しいかんじですね。（グラフの描画ごとに下位の数値が変わるとかいう技もございますが･･･）

　数値の正確さ求めるばやいに愚生がたよりにしているのはOEISさんなのですが、以上の２つについては「お出ましなし」（または捜索不備？）で、やはりマイナーなグレープの数値であるようです。

≪３≫　今日では等高グラフは、いきなりGeoってみて、こんな感じ。

　　　　

　ということで、わかくさみずいろ色っぽいレムニ型の場合の数式は？といえばこれ。

　　　　

　さらに、ｃの値をｚ軸（見やすいように、記事と同じく下方がプラス）としたGeo版３Dグラフも載せておきましょう！　ひょっこりひょうたん島風になってきました！！

　　　　

　　　　

[参考書]

［１］山下純一、２点からの距離の「何とか」が一定な点の軌跡、現代数学、現代数学社、1977-11月号、ｐ４～

Ｋ、Ｒもゼータプライムで締めるの巻

≪１≫　先日の⚾WBCでいえば、最後の抑えにオータニさんが登場する感じで、昨日の多重連分数Ｋと、多重根号Ｒにもゼータさんに登場いただきました。投げる球種は、ｎ+1とｐｎの2種類。

≪２≫　引き続き裏方のWolframさんに、ｎ＝15あたりまで頑張ってもらい、そのけっかは以下のとおり。

　すなわち、

　　　　

　　　　

　　　　

　　　　

となるのは、計算数値で順に

　　　   0.45407･･･

　  　0.45491･･･

　　  1.82563･･･

　　  1.82424･･･

ですと。

　いずれも天下のOEISさんに見当たらないのは、まだ数値が違うのか、はたまたマイナー度の度合いが過ぎるのか｡｡｡

ついにはプライムゼータをタワーリングする巻

≪１≫　数列の無限和や無限乗積で、最後はどうなるのかって思うのはすごく楽しいことですね。今回は、和や積以外の演算の多重積み重ねでもってその結末を楽しむというツアーとなります。

　和の記号 ∑ 、積の記号 Π にならって、ここでは累乗をＴ、連分数をＫ、多重根号をＲで表したいと思います。連分数のＫだけは、マイナーではありますがWolframなどでも使用されてる正式な数学記号ですね。（あとの２つは、自家製のものですんで）

　　　　　

　　　　　

　　　　　

　どれもｎ＝１から ∞ を考えますが、表記は省略しています（メンドウなため）。また K ではｂｎ=１というのが「正則」だとか称されて、よく扱われるのも有名かと。 　

　今回はこれらそれぞれの演算に、定数や自然数列、素数列をいれると、さてどないなことになるんやろかという内容でございます。

≪２≫　で、まずは累乗タワーのＴ。素朴な直観では、収束にはａｎ→１が必要と思われますが、真実はさにあらず、0.065･･･から1.444･･･のあいだの一定数なら収束すると。（数学定数事典、ｐ452～など）

　有名どころは、ａｎ＝√２（＝1.414･･･）の場合。これの極限値が２とのことで、これはこれでシブいです（遠くへ行ってしまうと思いきや、実家がえりみたいな微妙な感じ）。

　つぎにａｎ＝1/（ｎ+1）のばあい。つまり、

　　　　

前掲書によれば、これは偶数・奇数で0.658･･･と0.690･･･とに「２値収束」するとのこと（ただし、正式用語法ではこれは「発散」扱い）。OEISではA242759と60です。

　そして、ａｎ＝素数列ｐｎのばやい、

　　　　

この場合も収束値は偶数・奇数で分かれ、0.719･･･と0.609･･･ですと。（OEISでA117493と92に登場）

　どちらも、ぱっと見では収束するのかすら分からない点とか、２値収束しちゃうなんてところが、じわります。

≪３≫　つぎに連分数Ｋさん。定数ａｎ＝１；

　　　　　

は、これまた著名な黄金比 φ＝1.61803･･･(OEIS　A001622、数学定数事典ｐ5～)より１をさっぴいたもの、あるいは黄金比の逆数 1/φ とも言われます。

　つぎに、ａｎ＝ｎのばやい、それとａｎ＝素数ｐｎのばやいはそれぞれ、

　　　　　

　　　　　

となり、数値は0.69777･･･（A052119　Ｃ１、連分数定数との愛称がついてると）、および0.43233･･･（A084255　愛称不詳、連分数定数の素数版とでも）ですと。

≪４≫　駆け足ですが今回のトリ、多重根号のＲさん。定数１、自然数、素数の順に登場いただきましょう。

　　　　　

　　　　　

　　　　　

それぞれの数値は、黄金比φ、1.75793･･･（A072449　数学定数事典ｐ8）、2.10359･･･（A105546）とのことであります。

≪５≫　上記の演算さんらは、理論的にはすでにいろいろと探求されているようでして、また変種亜種も多種にわたっているようです。このせいか、今回求めた数値は、すべて既知のものばかりでした。未知の数ハンターとしてはやや残念な面もございます。

　そこで、アンコールにお応えしてOEISにも未登場（探しきれてないだけ？）の新曲２つを紹介して、マクとさせて頂きましょう。 ζ（ｎ）は泣く子も黙るゼータカンスウで、これをタワーリングしてみますと、、、

　　　　

　　　　

実験での数値は、1.83630･･･と1.82645･･･です。どちらも、OEISさんではhitせず、Wolfさんに計算して頂いた（途中？ｎ＝15までの）結果でありますます。どっかに出ているのを発見されたら、ぜひとも御教示くださいませ。

〈参考〉

・数学定数事典（朝倉書店）　その名のとおり、定数の宝庫。いつもながらお世話に　　なっております。

・OEIS　　リンク先のMathWorld含め、お世話になっております。

・Wolfram　　ゼニもはらってないのに、最後の計算とかも、文句も言わずにやってくれます。Z世代とは、えらい違いや～🤗