≪1≫ 平面上に2点があって、そこからの距離の 和 が一定な曲線は?といえば、楕円。 積 が一定なら?といわれりゃレムニスケート!
なら、ベキならどうなの?という記事が、これまた半世紀まえ(正確には45年前)の雑誌「現代数学」[1]にありました。
記事の著者山下先生も、当時の最新型計算機?HITAC-10を最大限に活用されて数値の計算やそのグラフ化をされておられ、いま読み返してみますと計算機性能の違いにやはり隔世感を味わえ、じわります。

(写真はweb「日立評論1969年11月号:超小形電子計算機 HITAC 10」より。当時価格で、約500マンエンとのことデス。)
本日は、ベキの場合を今日的アイチムでもって焼き直してみて、数値や形状グラフを再堪能してみるという回顧型記事となります。
≪2≫ 2点を(-1,0),(1,0)とれば、距離はそれぞれ
A=√((x+1)^2+y^2)、B=√((x-1)^2+y^2)
となり、式A^B=cを満たす点の集まりが、今回の曲線となる。
当時の記事では、まずはcの値ごとに該当点(x、y)を平面上にプロットしていくというなかなか手の込んだ手法で概形を推測していくという方法ですが、当時はこれしかないので致し方ございません。
ここは是非、若い読者のみなさんにも、当時の昭和の苦労感を堪能してもらえればとの意向で、記事の図の一部を引用させていただきましょう。

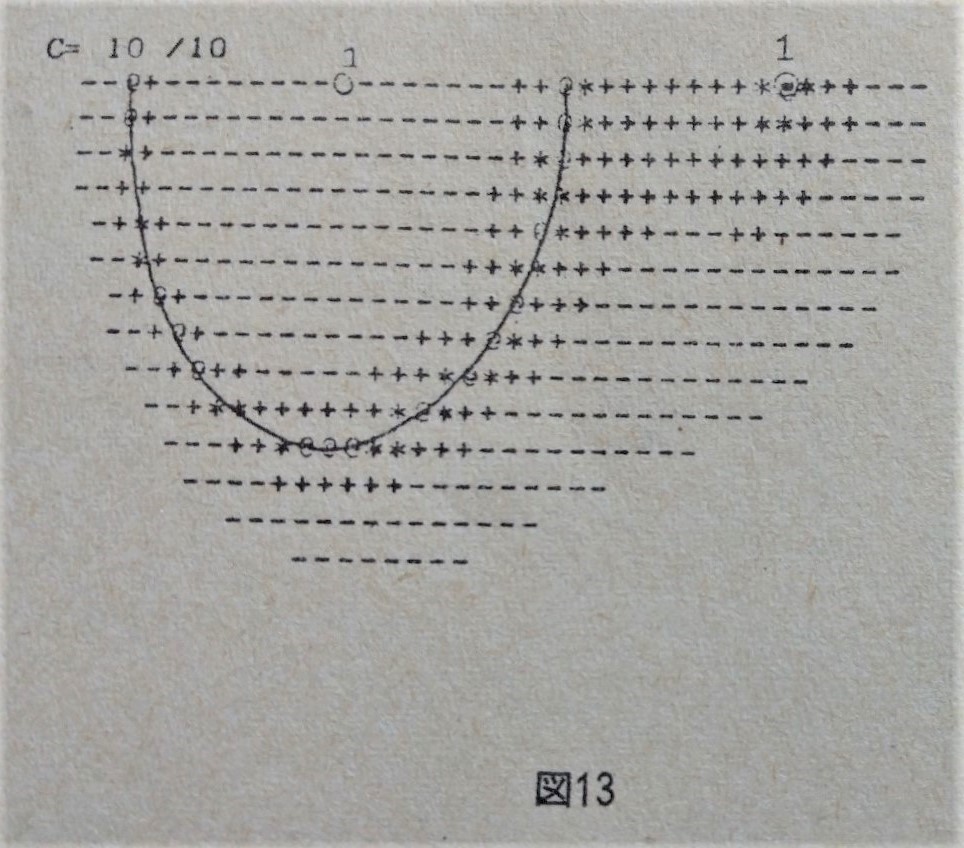
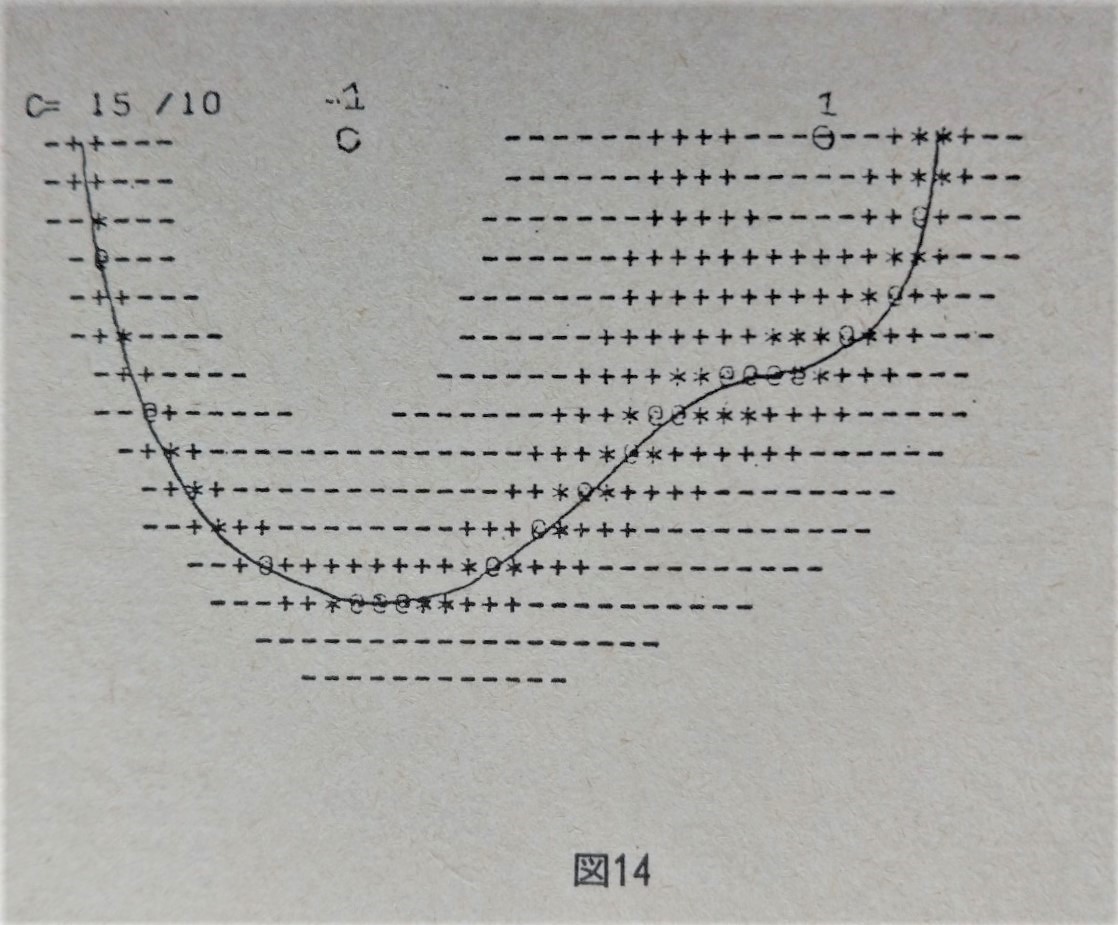
こういうのをいっぱい作成して、やっとこさ次のような予想概形の図にたどり着く、というプロセスになる。
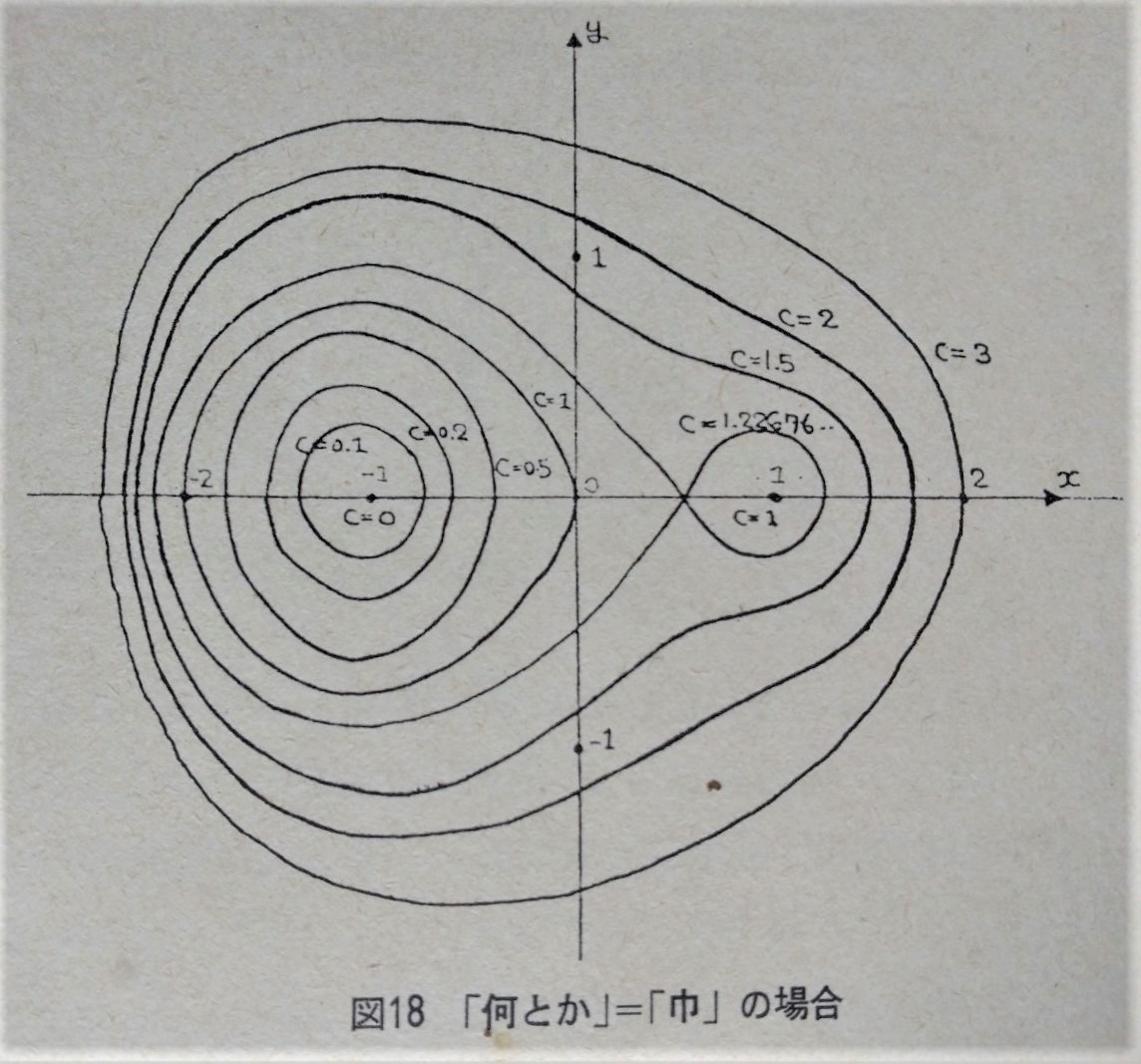
cの値は、外側から順に
3、2、1.5、
1.22676・・・、
1、0.5、0.2、0.1、0
で、1.22676・・・のところでレムニ型が生成されているのが観察されます。
概形がつかめたら次はレムニスケート風になりそうなポイントを正確に探すために、
稜線y=0での切断面のグラフと、あと、それを微分した式=0から極点を導出するという王道手順。つまりy=0とした ![]() の極点を捜索していくことになります。(タテ軸がcです)
の極点を捜索していくことになります。(タテ軸がcです)
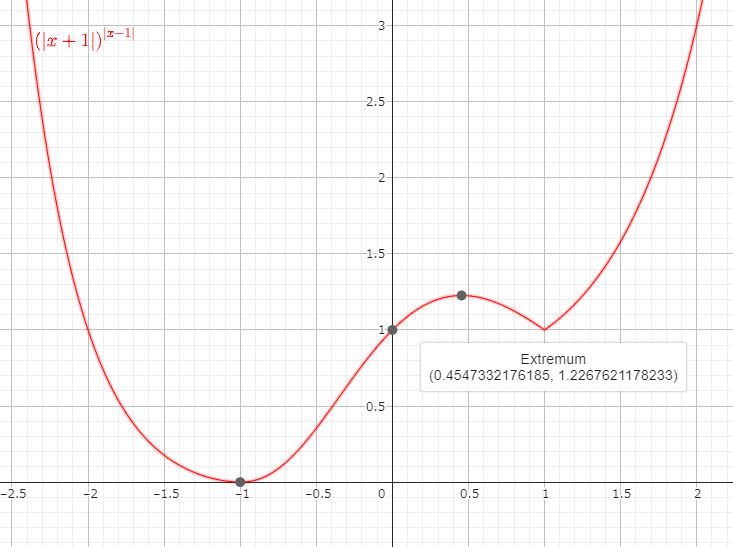
ここで、Wolfさんらにも登場いただき算出された各数値を比較してみて、正確さの「経年優化」のどあいを見比べてみましょう。まず極大となるxの値はといいますと
・記事 0.45473 321・・・
・Wolf 0.45473 32175 61064・・・
・Geo 0.45473 32176 185・・・、
また、このときのcの値は
・記事 1.22676 213・・・
・Wolf 1.22676 21178 23279・・・
・Geo 1.22676 21178 233・・・
となっていて、小数点以下7位くらいまでは当時のものでも正確だと見受けます。なお、Geoさんで表示してくれるextremumエクストゥリマム(極値)も、いつもですが、同じく7位くらいまでが正しいかんじですね。(グラフの描画ごとに下位の数値が変わるとかいう技もございますが・・・)
数値の正確さ求めるばやいに愚生がたよりにしているのはOEISさんなのですが、以上の2つについては「お出ましなし」(または捜索不備?)で、やはりマイナーなグレープの数値であるようです。
≪3≫ 今日では等高グラフは、いきなりGeoってみて、こんな感じ。
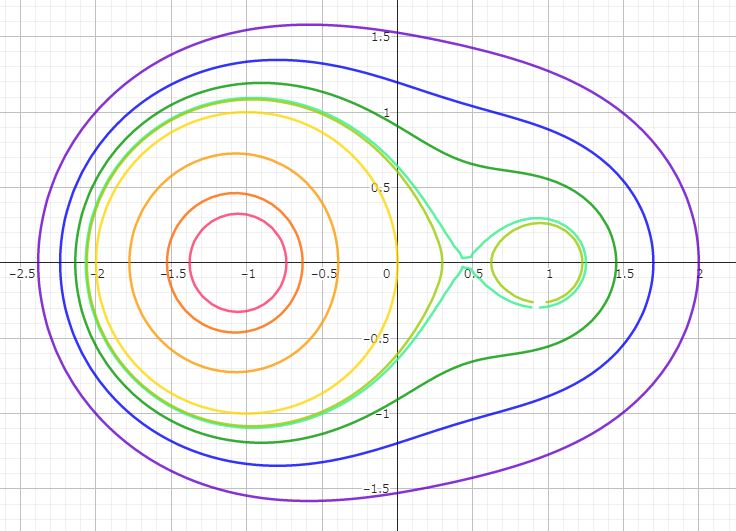
ということで、わかくさみずいろ色っぽいレムニ型の場合の数式は?といえばこれ。
![]()
さらに、cの値をz軸(見やすいように、記事と同じく下方がプラス)としたGeo版3Dグラフも載せておきましょう! ひょっこりひょうたん島風になってきました!!
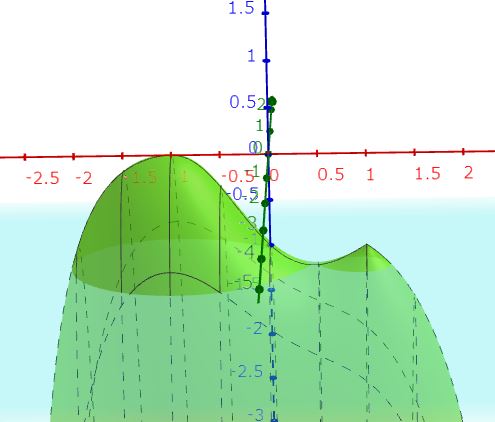

[参考書]
[1]山下純一、2点からの距離の「何とか」が一定な点の軌跡、現代数学、現代数学社、1977-11月号、p4~