半世紀の隔世感を堪能する

≪１≫　いまの世のなか、なんでもかんでもPCやスマホに依存しているわけで、愚生もそのひとり。（といってもその入り口あたりですが）数学のなかの一分野、「数値の計算」なんぞはまったくこのデジタルの世界の得意分野でありますね。

　中世のニュートンとかオイラーやガウスの膨大な計算記録を眺めていると、この方々の時代に現代のPCとかがあったら一体どんなことになっていたんだろうと想像してしまいます。つまり、彼らが数値計算に費やしていた時間をもっと別の研究時間に費やしていたら、、、と。（逆に、その計算を楽しむことで、偉大な業績のもとになったとも考えられますが）

　本日は、いまから半世紀まえあたりに小生が遭遇した数学の問題を、現在の観点で見つめなおしてみるとどんな感覚を味わえるか？というこころみとなります。

≪２≫　ひとつめの出し物は、有名な「ケプラー-ボウカンプ定数」というもので、

　　　　・単位円からスタート。それに内接する正３角形を書く

　　　　・それの内接円を書き、さらに内接する正３+１＝４角形を書く

　　　　・以下これを繰り返す。このとき極限円の半径は？ゼロか？

　　　　（図はhttps://en.wikipedia.org/より）

というもので、コタエの数値は意外にもゼロではなく、ρ＝0.11494･･･とのこと。

　これを求める数式は、

とのことで、π/3つまり60°のcos＝0.5からはじまり、１に近づく数の乗積なのですが、実はこれの収束がめっちゃ遅い、と。

　で、「これの数値を（せめて小数点以下３けた位まで）求めなさい」という出題が、むかしの数セミ「エレガントな解答をもとむ」に出ていました。これの出題自体は1971年で、小生は直接見たわけではなく1978年刊行の第２集で遭遇したわけです［１］。（どっちゃににしても、いまから50年くらいまえのことですが･･･😅）

　図形的な考察から上記 cos の式を導出したら、今日的にはいきなりWolframとかにかけてみたくなる。乗積 Π も準備されてるWolfの（むらさき色の）画面に、ポイポイと入力すると、ひょこっと出てくる。

こんどはその数値の始めの方5，6ケタ程度をOEISで検索するとメデタク hit。（⇨OEIS　A085365）歴史的背景や関連情報なども、これでもかと付いてくる。別名が多角形内接定数だとか、どなたかは「多角形の井戸に落ちる」なんて表現してるとも。（井戸のほうは残念ながら、404😢）

　半世紀まえの時点では、おそらく電子計算機を使えるというのは一部の高級な人で、ふつーの人は、電卓や数表を活用したりで苦労されてたと思います。上記の出題の当時の解説欄では「電子計算機を用いれば何でも計算出来ると思ってはいけない。直接、式を計算したのでは･･･（計算機でも）いつまでたっても2～3桁しか答が得られないであろう」とも。

　つまり、計算機にかけるまえにしっかりと数式の評価をせんといかんよという趣旨の出題ですね。これはこれで大事なことですが、計算機の能力については格段の差が生じてしまっていて、隔世感を味わえます。

≪３≫　ふたつめの出し物は、同じく「エレガントな･･･」のこんどは第３集に出ていたもので、次の関数の最大値を与えるｘを求よ、との出題。

　いまの小生がこういうときに使うのは、いきなりのグラフソフトGeoGebra。式を入力すれば、グラフが（わりあい）正確に描画され、たいがいの場合、最大点や零点なども拾ってくれます。

　今回のは、問題にされた最大点を含め、こんな感じ。あっという間のティファール。結果を知れば、あとはその導出に専念できる。ここでも隔世感100％。

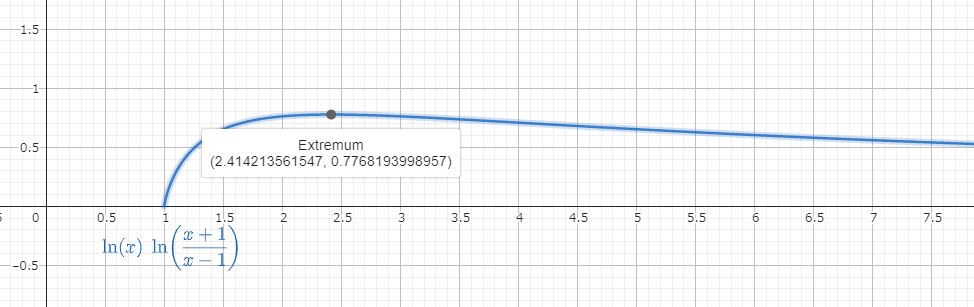
　このｘの小数点以下の数値はみんなが見覚えがあるもので、コタエは1+√２なんでは？と推定。問題自体はそこで確かに最大となるというのを論証していくというのが出題の主眼のようです。出題者は「何でもビブンしてそれの零点前後の評価？それでイケるかな？」とも。

　解説記事には最後にグラフもついているのですが、当時のフツーのひとにはそんなグラフを描く手段は極少。電卓でlogの数値を書き出し、その数値を方眼紙にプロットしフリーハンドでもって滑らかに繋いでいくという方法で過ごした方も多いのでは？できた曲線をながめてはニヤニヤしていた時代が、小生にもありました。これではないのですが、一例として、ｙ＝ｘ^ｘ、ｘ^ｘ^ｘ、･･･のグラフを、手描き版とGeo版とを載せておきましょう。ここもカクセイ感が･･･。