≪1≫ ふるい時代の公式集やテキストをながめていると、現在の視点からはやや違和感のある内容がありますよね。愛用の岩波数学公式なんかでも、関数の数値表がガッツリあったり(特にⅢ)、平面曲線がたくさんのっていたり(Ⅰとか)。計算機というのがまだまだ特別な時代でしたので、これは致し方ございません。
現在は、PCやスマホでもつかってパパっと、それこそなんでも出てくるドラえもん時代。そんな時代で、ジブンがちょっとはまった「落とし穴」っぽい事例を、記事にしたいと思います。本来、実験数学の世界なんですが「キバツな事例」にはならなかった事例とも言えます。
≪2≫ 例として、下記をもってきました。
![]()
Geoを活用して、いきなり立体図と平面図を紹介しますとこんなかんじです。

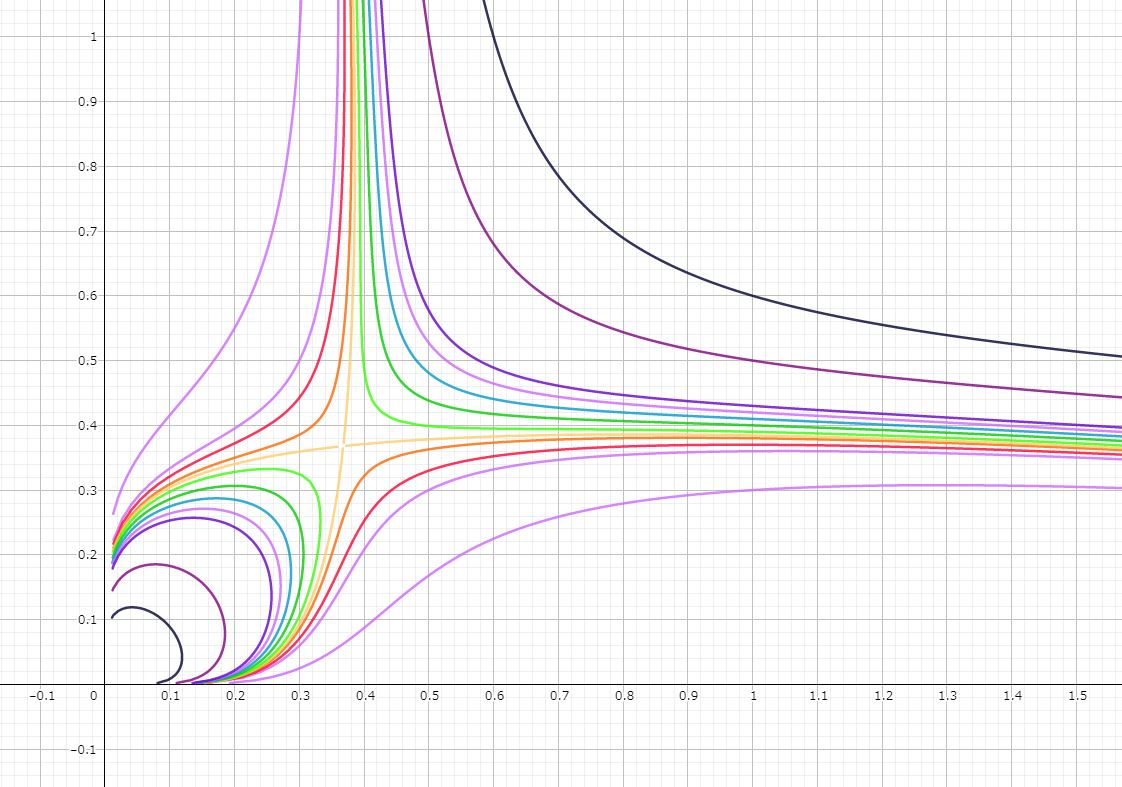
≪3≫ 鞍点(あんてん、サドルポイント=平面のほうで黄色の線の交点のところ)が気になるということで、正攻法ではx、yで偏微分→この零点が候補・・・で、x=y=1/e をひっぱりだし、なんとかの判定でもって結局のところ、

とういのが出てくる次第です。この数値だけなら、立体のほうでy=xのところの稜線(分水嶺)を考え、これはおなじみの曲線 y=x^x での例の最小値の2倍、と考えた方が近道かもですね。(こっちのほうが高校の範囲でイケる?)
≪4≫ 小生は、はじめ平面Geoでのクツロギモードで、x^y+y^x=?のグラフをいろいろ描いていました。(上図のカラフルなところ)すると、z=1.38 過ぎあたりでグラフの「くっつきかた」が変わるポイントがあったわけで、定数サーチャーとしては「これは新型定数では?」と息巻いた訳です。
しかしながら、これは冷静に立体で考えてみると上記のとおり単純な鞍点通過の現象と判明し、一件落着シャンシャン😅 PCで遊んでいると、いろんなものがパパッと出てくるのですが、こういう点は自分自身への警鐘としたいとおもう今日この頃であります。
≪5:ふろく≫ まぁ、これはこれとして近年思うのは、鞍点(峠点)とか稜線・分水嶺といったところは、なるべく実際の山を歩くなどで全身で体感したいという点ですね。できれば幼少時から小学生あたりまでで。そういう原初体験が、その子の今後の人生、先々でもきっと役立つと思うんですがどうでしょう。
世間では小学校などからデジタル化が加速されようとしていますが、こういうのもお願いしますね、文科省さん。